tour de hanoi 9 disques

• Boites secrètes
• Casse-tête et Puzzle
• Jeux multi et famille
• Coffrets bois
• COFFRETS / CADEAUX
• JEUX DE RÉFLEXION
• CASSE-TÊTE ENFANTS
• CASSE-TÊTE EN MÉTAL
• CUBE / AUTRES FORMES
• CASSE-TÊTE BOUTEILLE
• HANAYAMA Métal

Règle du jeu : La Tour de Hanoï

• 46101 views

La Tour de Hanoï, présentation et règles du jeu.

La Tour de Hanoï est un grand classique dans l'univers des casse-têtes. Vous en avez certainement déjà croisé une ! Malgré les différentes variantes et formes existantes, le but reste le même : déplacer la Tour en un minimum de coups d'un point A à un point B. Mais pas si simple !

La Tour de Hanoï est un puzzle, ou jeu mathématique, inventée en 1883 par Édouard Lucas, arithméticien français né à Amiens, professeur à Saint-Louis, et connu notamment pour ses travaux sur la théorie des nombres et ses Récréations mathématiques . Il prouvera d'ailleurs sa passion pour les jeux mathématiques et de réflexion en commercialisant son casse-tête sous le nom de N. Claus de Siam , professeur au collège de Li-Sou-Stian et prétendument son ami. Mais pour les plus perspicaces d'entre vous, vous aurez compris que ce pseudonyme est en réalité l'anagramme de son nom ( Lucas d'Amiens ) et de la ville où il enseignait ( Saint-Louis ).

Les Tours de Hanoï sont également connues sous le nom de Tours de Lucas ( vous savez maintenant pourquoi ! ), ou Tours de Brahma. Brahma était le dieu créateur-démiurge de l'hindouisme, le premier membre de la Trimūrti, la trinité des déités hindoues majeures. Les autres membres sont Vishnou et Shiva.

La légende se passe au cœur du temple Kashi Vishwanath. Elle raconte que Brahma, au commencement des siècles, apporta dans ce temple, sous le dôme doré au centre du monde, 3 aiguilles de diamant, plantées dans une dalle de bronze, et 64 disques d'or pur, le plus large reposant sur l’airain, et les autres, de plus en plus étroits, superposés jusqu’au sommet. C'est la Tour sacrée de Brahma.

Les règles de Brahma sont simples : les prêtres doivent déplacer la tour de la première à la troisième aiguille, en ne déplaçant qu'un disque à la fois. Le disque déplacé doit l'être sur l'une des 2 autres aiguilles, et ne doit jamais être placé au-dessus d’un disque plus petit que lui. Nuit et jour, les prêtres se succèdent sur les marches de l’autel, occupés à transporter la Tour de la première aiguille sur la troisième. Lorsque les prêtres auront terminé, la tour et le temple tomberont, et ce sera la fin des mondes !

Si nous étudions les algorithmes de résolution de la Tour, le nombre de mouvements nécessaires pour déplacer les 64 disques de la première à la troisième colonne est de 18.446.744.073.551.615. Si on considère que les prêtres mettent 1 seconde pour déplacer 1 disque, il faudra plus de 5 milliards de siècles ( 5.845.580.504 exactement ! ) pour terminer la Tour. La fin du monde est encore loin !

A travers cette légende, certains pensent que Lucas fait ici encore parler sa passion pour les jeux et la réflexion.

Pas d'anagramme cette fois, mais des similitudes troublantes entre le nom du temple « Kashi Vishwanath » et le nom de l'ex champion du monde d'échec indien Viswanathan Anand. Et que dire de sa version géante de la Tour de Hanoï avec ses 64 disques … 64 … qui correspond au nombre de cases d'un échiquier …

RÈGLE DU JEU

On dispose de 3 piquets fixés sur un socle, et d'un nombre n de disques de diamètres différents. Les disques sont empilés sur un piquet, en commençant du plus large au plus petit. Le nombre de disques peut varier. Plus il y a de disques au départ, plus le jeu est difficile.

Déplacer les disques d'une tour de 'départ' à une tour 'd'arrivée' en passant par une tour 'intermédiaire', et ceci en un minimum de coups.

2 règles simples :

- on ne déplace qu’un seul disque à la fois, et le disque déplacé doit l'être sur l’un des deux autres piquets au choix ; c’est ce que l’on appelle un déplacement.

- le disque déplacé ne doit jamais être placé au-dessus d’un disque plus petit que lui.

La solution générale est donnée par l'algorithme suivant.

Algorithme récursif

La solution de base du jeu de la Tour de Hanoï est formulée de manière récursive. Étiquetez les piquets avec A - B - C et numérotez les disques de 1 (le plus petit) à n (le plus grand). L'algorithme est exprimé comme suit:

1. Déplacez les n-1 premiers disques de A à B. (Cela laisse le disque n seul sur le piquet A) 2. Déplacez le disque n de A à C 3. Déplacez les n-1 disques de B à C

Pour déplacer n disques, il faut effectuer une opération élémentaire (déplacement d'un seul disque) et une opération complexe, c'est-à-dire le mouvement de n-1 disques. Cependant, cette opération se résout également de la même manière, en demandant comme opération complexe le déplacement de n-2 disques. En itérant ce raisonnement on réduit le processus complexe à un processus élémentaire, c’est-à-dire le déplacement de n-(n-1)=1 disque. C'est un algorithme récursif de complexité exponentielle.

Il est intéressant de noter que le casse-tête peut être résolu pour n'importe quel "n", avec une démonstration par récurrence: supposons que nous ayons une tour en A composée de N disques, et supposons que N soit le nombre de disques maximum autorisés à résoudre le jeu. Au terme du déplacement de la tour de A à B, nous ajoutons à A un disque supplémentaire, de taille égale à N+1, et supposons que ce disque ait été arrêt tout le temps sous les autres. À ce stade, nous déplaçons simplement le disque de A à C, et nous pourrons certainement déplacer la tour de B à C en suivant les mêmes étapes que celles qui étaient nécessaires pour le faire de A à B. Après avoir montré qu’une tour de N disques peut être déplacée d’une colonne à une autre, il est également montré qu’on peut déplacer une tour de N+1 disques.

Aspects psychologiques

Ce casse-tête est utilisé en particulier dans la recherche psychologique, à travers la résolution des problèmes. Il est également utilisé comme test neuropsychologique.

Ce test peut détecter les mauvais fonctionnements des zones frontale et préfrontale et permet d’évaluer les fonctions exécutives telles que la planification, le travail, la mémoire et l’inhibition. La résolution du jeu de la Tour de Hanoï dépend de l'activité inhibitrice, de la "mémoire de travail", c'est-à-dire l'utilisation de la mémoire à court terme, de la mémoire procédurale et de l'intelligence fluide. Ce test est similaire à celui de la Tour de Londres, ainsi qu'à celui des Tours de Toronto, utilisé avant tout pour évaluer les compétences de décision stratégique et résolution de problèmes chez les enfants de 4 à 13 ans et pour étudier les effets du vieillissement sur la résolution des problèmes simples.

Le casse-tête de la Tour de Hanoï est très joué en ligne, on peut trouver de nombreuses réalisations pour ce jeu, en Flash et en Java.

Related products

3 casse-têtes en bois - coffret cadeau - jeu casse-tête plusieurs niveaux, carré royal casse-tête composé de plusieurs essences de bois, jeu de logique et réflexion en bois les 5 différents, jumanji escape room le jeu, édition familiale escape game 3 aventures, tour de hanoi 7 pièces casse-tête en bois.

En poursuivant votre navigation , vous acceptez l'utilisation de cookies.

Outils mathématiques pour le lycée

Grand oral : les tours de hanoï.

Cet article traitera de l’énigme des trous de Hanoï. Il ne s’agit pas d’un sujet de grand oral donné clé en main, mais simplement d’une présentation du problème et de sa résolution, en lien avec le programme de mathématiques de Terminale Générale.

Il ne tient qu’à vous de sélectionner les informations qui vous semblent pertinentes sur cette page et d’en chercher de nouvelles ailleurs pour constituer votre oral.

Thèmes abordés

• Suites et récurrences
• Un peu de dénombrement pour la variante
• Peut-être choisi pour un oral croisé Mathématiques – NSI

Présentation de l’énigme

L’énigme des tours de Hanoï est un jeu de réflexion imaginé par le mathématicien Edouard Lucas.

Ce jeu est composé de trois piquets ainsi que d’un certain nombre de disques de diamètres différents, originellement tous placés sur le premier piquet. Le but est de transférer ces disques du premier au troisième piquet, en suivant deux règles

• on ne peut déplacer d’un seul disque à la fois ;
• il n’est pas possible de placer un disque sur un autre disque plus petit

Vous pouvez ci-dessous essayer de résoudre cette énigme vous-même avant de vous lancer dans la suite de l’article.

Résolution récursive du problème

Algorithme récursif.

Une manière classique pour résoudre l’énigme des tours de Hanoï est de procéder de manière récursive. Nous allons montrer par récurrence que l’énigme du tour de Hanoï à \(n\) disques possède bien une solution.

• Initialisation : Pour 1 disque, il est assez facile de résoudre ce problème…
• Nous déplaçons les \(n\) disques du sommet du piquet A au piquet B. C’est possible en \(t_n\) coups, d’après notre hypothèse de récurrence.

• Nous déplaçons le disque restant du piquet A au piquet C. Cela ne demande qu’un seul coup.

• Nous transférons alors les \(n\) disques du piquet B au piquet C. Cela demande de nouveau \(t_n\) coups.

• Conclusion : \(P(1)\) est vraie et \(P\) est héréditaire. Par récurrence, \(P(n)\) est vraie pour tout entier naturel non nul \(n\).

Cette démonstration nous permet par ailleurs de déterminer une relation de récurrence sur la suite \((t_n)\), qui est définie ainsi : \[ \left\{\begin{array}{l}t_1 = 1\ \\ \text{Pour tout entier naturel }n,\, t_{n+1}=2t_n+1\end{array}\right.\]

Nous pouvons alors calculer les premiers termes de la suite \((t_n)\).

• \(t_1 = 2t_0+1 = 2 \times 1 +1 = 3\)
• \(t_2 = 2t_1+1 = 2 \times 3 +1 = 7\)
• \(t_3 = 2t_2+1 = 2 \times 7 +1 = 15\)
• \(t_4 = 2t_3+1 = 2 \times 15 +1 = 31\)

Il semblerait que pour tout entier naturel \(n\), \(t_n=2^n -1\). Deux méthodes sont envisageables pour le démontrer

Montrer par récurrence que, pour tout entier naturel non nul \(n\), \(t_n=2^n-1\).

Méthode 2 :

• Déterminer le réel \(r\) tel que \(r=2r+1\)
• Montrer que la suite \((x_n)\) est géométrique
• Exprimer \(x_n\) puis \(t_n\) en fonction de \(n\)

Pour tout entier naturel non nul \(n\), nous considèrons la proposition \(P(n)\) : « \(t_n =2^n-1\)».

• Initialisation : Pour \(n=1\), on a \(2^1-1=2-1=1=t_1\). \(P(1)\) est vraie.
• Hérédité : Soit \(n\) un entier naturel non nul. Supposons que \(P(n)\) est vraie. Alors, \(t_n=2^n-1\). Or, \[t_{n+1}=2t_n+1=2 \times(2^n-1)+1=2 \times 2^n-2+1=2^{n+1}-1\] \(P(n+1)\) est vraie.
• Soit \(r\) un réel. \(r=2r+1 \Leftrightarrow -r = 1 \Leftrightarrow r=-1\)
• Pour tout entier naturel non nul \(n\), \[x_{n+1}=t_{n+1}+1=2t_n+1+1=2(t_n+1)=2x_n\] La suite \((x_n)\) est géométrique de raison 2
• Pour tout entier naturel non nul, on a \(x_n = x_1 \times 2^{n-1}\) c’est-à-dire \(x_n=2 \times 2^{n-1}=2^n\) et donc \(t_n=x_n-1=2^n-1\)

Exemple de résolution

Prenons l’exemple de la résolution de l’énigme de la tour à 3 disques. D’après l’algorithme récursif il faut :

• Déplacer les 2 disques du sommet du piquet A au piquet B
• on commence par déplacer le disque du sommet du piquet A au piquet C
• On déplace ensuite le deuxième disque du piquet A au piquet B
• On place alors le plus petit disque, situé au piquet C, sur le disque au piquet B
• On peut alors déplacer le disque numéro 3 du piquet A au piquet C
• Il faudra alors déplacer la tour de 2 disques situés au piquet B vers le piquet C
• Pour cela, on commence par déplacer le disque du sommet du piquet B au piquet A
• On déplace ensuite le deuxième disque du piquet B au piquet C
• On place alors le plus petit disque, situé au piquet A, sur le disque au piquet C

Les mouvements à effectuer sont donc les suivants

• Disque 1 : A → C
• Disque 2 : A → B
• Disque 1 : C → B
• Disque 3 : A → C
• Disque 1 : B → A
• Disque 2 : B → C

Vers une solution itérative

La résolution récursive possède un grand désavantage : bien que l’on sache qu’il est possible de résoudre le problème, il est difficile d’établir directement et de tête la liste des coups.

Une fois la méthode prise en main, et en augmentant le nombre de disques, on remarque aisément que le plus petit disque est déplacé tous les 2 coups.

En effet, lorsque l’on déplace le petit disque d’un piquet à un autre, il n’y a alors que deux disques de libre. Nous sommes alors obligés de déplacer le plus petit de ces disques sur le plus grand de ceux-là.

Mais alors :

• Il n’est pas possible de déplacer le disque que nous venons de déplacer, sans quoi la solution n’est plus optimale
• Il n’est pas non plus possible de déplacer le disque qui se trouvait en-dessous, puisque les deux autres disques sont plus petits

Le seul choix restant est alors de déplacer le petit disque.

Le nombre total de coups étant de \(2^n -1\) pour la solution optimale, cela signifie que le petit disque se déplace \(2^{n-1}\) fois, que le disque numéro 2 se déplace \(2^{n-2}\) fois et ainsi de suite, jusqu’au plus gros disque qui ne se déplace qu’une fois.

On retrouve ici l’égalité \( 1 + 2 + 4 + \dots + 2^{n-1} = 2^n -1\).

Il suffit alors de savoir les mouvements du plus petit disque pour résoudre de manière itérative le problème des tours de Hanoï. Dans le cas de la résolution avec 3 disques, les mouvements du disque 1 étaient A → C → B → A → C. Pour le problème à 4 disques, les mouvements de ce plus petit disque s’effectueront en revanche dans l’autre sens A → B → C → A …

• Si le nombre \(n\) de disques est impair, déplacer le plus petit disque une fois sur deux dans le sens A → C → B → A
• Si le nombre \(n\) de disques est pair, déplacer le plus petit disque une fois sur deux dans le sens A → B → C → A

Pour les autres coups, effectuer l’unique déplacement possible n’utilisant pas le plus petit disque.

Variante : Passer par toutes les positions

Nous avons jusqu’ici uniquement traiter la solution optimale, c’est-à-dire celle qui demande le moins de coups possibles. Une autre possibilité serait de résoudre le problème des tours de Hanoï en passant par toutes les positions possibles.

Il est possible de placer le plus gros des disques sur n’importe lequel des 3 piquets. Puis, le disque suivant peut lui aussi être placé sur n’importe quel piquet, puisqu’il n’y a pas de disque déjà positionné, et ainsi de suite jusqu’au plus petit.

Une configuration de l’énigme des tours de Hanoï peut être vue comme un \(n\)-uplet de l’ensemble \(\{A;B;C\}\) ou le \(k\)-ième coordonnées désigne l’emplacement du disque numéro \(n-k\). De ce fait, le nombre de configurations valides est de \(3^n\).

Pour les élèves suivant l’option Maths expertes : les positions peuvent alors être placées dans un graphe : deux configurations sont reliées s’il est possible de passer de l’une à l’autre en un seul coup. Trouver une solution au problème de Hanoï qui passerait par toutes les configurations possibles revient donc à trouver un chemin eulérien dans ce graphe, ayant pour départ la configuration AAA…A et pour arrivée la configuration CCC…C

Là encore, il est possible de montrer qu’une solution existe de manière récursive :

• Avec un seul disque, il suffit de passer du piquet A au piquet B puis au piquet C
• On déplace les \(n\) premiers disques du piquet A au piquet C en passant par toutes les configurations
• On déplace le disque \(n+1\) du piquet A au piquet B
• On déplace les \(n\) disques du piquet C au piquet A, encore une fois en passant par toutes les configurations
• On déplace le disque \(n+1\) du piquet B au piquet C
• On déplace une dernière fois les \(n\) disques du piquet A au piquet C, toujours en passant par toutes les configurations

Sur notre graphe, cela revient à explorer la partie en bas à gauche du graphe, puis à emprunter l’arête bleue reliant ACC à BCC, explorer la partie haute du graphe, emprunter l’arête de BAA à CAA et enfin, explorer la partie en bas à droite du graphe.

Notre algorithme demande, pour la solution à \(n+1\) disques, de déplacer 3 fois une tour de \(n\) disques, et d’y ajouter 2 déplacements d’un seul disque. Si on note \(d_n\) le nombre de déplacements à effectuer pour \(n\) disques en passant par toutes les configurations valides, on aboutit à

\[ \left\{\begin{array}{l}d_1 = 2\ \\ \text{Pour tout entier naturel }n,\, d_{n+1}=3d_n+2\end{array}\right.\]

Les premiers termes de cette suite sont alors 2, 8, 26, 80… Il semblerait que pour tout entier naturel non nul \(n\), \(d_n=3^n-1\), ce qui est bien conforme à notre problème : puisqu’il y a \(3^n\) configurations valides, passer par toutes celles-ci demande \(3^n -1\) déplacements.

Partager cette page :

J’aime ça :, entrées similaires:.

Laisser un commentaire Annuler la réponse

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Commentaire *

Enregistrer mon nom, mon e-mail et mon site dans le navigateur pour mon prochain commentaire.

Les tours de Hanoï I : le problème classique

« La poste nous a remis récemment une petite boîte en carton peint, sur laquelle on lit : la Tour d’Hanoï, véritable casse-tête annamite, rapporté du Tonkin par le professeur N. Claus (de Siam), mandarin du collège Li-Sou-Stian. Un vrai casse-tête, en effet, mais intéressant. Nous ne saurions mieux remercier le mandarin de son aimable intention à l’égard d’un profane qu’en signalant la Tour d’Hanoï aux personnes patientes possédées par le démon du jeu. »  [ 1 ]

Le problème des tours de Hanoï a été inventé par le mathématicien français Édouard Lucas (1842-1891). Il est introduit de la manière suivante dans le tome 3 de son livre « Récréations mathématiques », qui a été publié à titre posthume en 1893  [ 2 ] .

Un de nos amis, le professeur N. Claus (de Siam), mandarin du collège Li-Sou-Stian, a publié à la fin de l’année dernière, un jeu inédit qu’il a appelé la Tour d’Hanoï, véritable casse-tête annamite qu’il n’a pas rapporté du Tonkin, quoiqu’en dise le prospectus. Cette tour se compose d’étages superposés et décroissants, en nombre variable, représentés par huit pions en bois percés à leur centre, et enfilés dans l’un des trois clous fixés sur une tablette. Le jeu consiste à déplacer la tour en enfilant les pions sur un des deux autres clous et en ne déplaçant qu’un seul étage à la fois, mais en défense expresse de poser un étage sur un autre plus petit. $\ $ $\ $

Lucas annonce donc que ce problème est dû à l’un de ses amis N. Claus (de Siam), mandarin du collège Li-Sou-Stian. On peut remarquer que « N. Claus (de Siam) » est l’anagramme de « Lucas d’Amiens », Amiens étant la ville natale d’Édouard Lucas, et « Li-sou-Stian » est celui de « Saint Louis », nom du lycée parisien où Lucas enseigne de 1879 à 1890. Après quelques observations sur ce problème, auxquelles nous nous intéresserons ensuite, il continue avec l’histoire, ou plutôt le mythe suivant.

LES BRAHMES TOMBENT ! Le mandarin N. Claus (de Siam) nous raconte qu’il a vu, dans ses voyages pour la publication des écrits de l’illustre Fer-Fer Tam-Tam, dans le grand temple de Bénarès, au-dessous du dôme qui marque le centre du monde, trois aiguilles de diamant, plantée dans une dalle d’airain, hautes d’une coudée et grosses comme le corps d’une abeille. Sur une de ces aiguilles Dieu enfila, au commencement des siècles, soixante-quatre disques d’or pur, le plus large reposant sur l’airain, et les autres, de plus en plus étroits, superposés jusqu’au sommet. C’est la tour sacrée de Brahma. Nuit et jour, les prêtres se succèdent sur les marches de l’autel, occupés à transporter la tour de la première aiguille de diamant sur la troisième, sans s’écarter des règles fixes que nous venons d’indiquer, et qui ont été imposées par Brahma. Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes !

Le problème classique

Reformulons maintenant ce problème de manière plus précise. Considérons trois piquets, notés $A$, $B$ et $C$, et un nombre fini de disques de tailles différentes que l’on suppose placés initialement par taille décroissante sur le piquet $A$. Le but est ici de transférer cette tour de disques du piquet $A$ au piquet $C$ en respectant les règles suivantes :

• un seul disque peut être déplacé à la fois,
• un disque ne peut être placé sur un disque de taille plus petite.

Par exemple, pour trois disques, on peut déplacer la tour du piquet $A$ au piquet $C$ en effectuant $7$ mouvements comme illustré ci-dessous.

Nombre minimal de mouvements

Nous allons ici déterminer le nombre minimal de mouvements $\mathrm{T}(n)$ pour déplacer une tour de $n$ disques du piquet $A$ au piquet $C$.

Pour $n=0$, on peut supposer que $\mathrm{T}(0)=0$ et pour un unique disque, il est évident que $\mathrm{T}(1)=1$.

Pour deux disques, il faut déplacer le grand disque du piquet $A$ au piquet $C$ et donc pour ce faire le petit disque doit être positionné sur le piquet intermédiaire $B$. Les trois mouvements suivants sont donc nécessaires et suffisants : le petit disque de $A$ vers $B$, le grand disque de $A$ vers $C$ et enfin le petit disque de $B$ vers $C$. On obtient donc $\mathrm{T}(2)=3$.

Par l’exemple proposé à la figure précédente, on sait que l’on peut déplacer la tour de trois disques en effectuant $7$ mouvements et donc $\mathrm{T}(3)\leqslant 7$. Montrons que l’on ne peut pas faire avec moins de mouvements :

• Pour déplacer le plus grand disque du piquet $A$ vers un second piquet, $B$ ou $C$, il faut préalablement déplacer les deux plus petits disques du piquet $A$ vers le troisième piquet, $C$ ou $B$ respectivement. Ce déplacement des deux plus petits disques nécessite au moins $\mathrm{T}(2)=3$ mouvements.
• Le plus grand disque est déplacé au moins une fois.
• Pour le déplacement final du plus grand disque vers le piquet $C$ à partir d’un second piquet, $A$ ou $B$, il faut préalablement que les deux plus petits disques soient positionnés sur le troisième piquet, $B$ ou $A$ respectivement. Après le déplacement final du plus grand disque, les deux plus petits disques sont alors déplacés du piquet $A$ ou $B$ vers le piquet $C$ et ce déplacement nécessite au moins $\mathrm{T}(2)=3$ mouvements.

Au total, nous venons de montrer que pour déplacer les trois disques $2\mathrm{T}(2)+1=7$ mouvements sont nécessaires et donc $\mathrm{T}(3)\geqslant 7$.

Ce résultat peut être généralisé pour tout $n\geqslant 2$.

\[ \mathrm{T}(n) = 2\mathrm{T}(n-1)+1 \text{ pour tout } n\geqslant 1. \]

Soit $\ n\geqslant 1$. Pour montrer que $\ \mathrm{T}(n) \leqslant 2\mathrm{T}(n-1)+1$, il suffit de proposer une solution utilisant ce nombre de mouvements. Considérons la solution suivante :

• les $\ n-1$ plus petits disques sont transférés du piquet $A$ vers le piquet intermédiaire $B$ en $\ \mathrm{T}(n-1)$ mouvements, le nombre minimal de mouvements pour déplacer $\ n-1$ disques d’un piquet à un autre,
• le plus grand disque est déplacé du piquet $A$ au piquet $C$ en $1$ mouvement,
• les $\ n-1$ plus petits disques sont transférés du piquet $B$ vers le piquet $C$ en $\ \mathrm{T}(n-1)$ mouvements.

Remarquons que cette solution pour $\ n=3$ correspond à celle de l’exemple précédent.

Montrons maintenant que $\ \mathrm{T}(n) \geqslant 2\mathrm{T}(n-1)+1$. La preuve est similaire à ce qui a été fait pour $\ n=3$.

• Pour déplacer le plus grand disque du piquet $A$ vers un second piquet, $B$ ou $C$, il faut préalablement déplacer les $\ n-1$ plus petits disques du piquet $A$ vers le troisième piquet, $C$ ou $B$ respectivement. Ce déplacement des $\ n-1$ plus petits disques nécessite au moins $\ \mathrm{T}(n-1)$ mouvements.
• Pour le déplacement final du plus grand disque vers le piquet $C$ à partir d’un second piquet, $A$ ou $B$, il faut préalablement que les $\ n-1$ plus petits disques soient positionnées sur le troisième piquet, $B$ ou $A$ respectivement. Après le déplacement final du plus grand disque, les $\ n-1$ plus petits disques sont déplacés du piquet $A$ ou $B$ vers le piquet $C$ et ce déplacement nécessite au moins $\ \mathrm{T}(n-1)$ mouvements.

Au total, nous venons de montrer que pour déplacer les $\ n$ disques $\ 2\mathrm{T}(n-1)+1$ mouvements sont nécessaires.

Cette preuve met donc en lumière la solution optimale du problème pour $n\geqslant 1$ disques, définie de manière récursive en fonction de la solution optimale pour $n-1$ disques.

Pour déplacer les $n$ disques du piquet $A$ vers le piquet $C$ en utilisant $\mathrm{T}(n)$ mouvements, on procède de la manière suivante : les $n-1$ plus petits disques sont transférés du piquet $A$ vers le piquet $B$ en $\mathrm{T}(n-1)$ mouvements, le plus grand disque est déplacé du piquet $A$ au piquet $C$ en $1$ mouvement, les $n-1$ plus petits disques sont transférés du piquet $B$ vers le piquet $C$ en $\mathrm{T}(n-1)$ mouvements.

La formule ainsi obtenue nous permet de calculer $\mathrm{T}(n)$ pour toute valeur de $n$ mais pour $n$ très grand, cela prend beaucoup de temps. Heureusement, il est possible de donner une formule explicite de $\mathrm{T}(n)$ en fonction de $n$.

\[ \mathrm{T}(n) = 2^n-1 \text{ pour tout } n\geqslant 0. \]

Pour $n=0$, on a $\mathrm{T}(0)=0=1-1=2^0-1$. Pour $n\geqslant 1$, on sait que $\mathrm{T}(n)=2\mathrm{T}(n-1)+1$ et donc \[ \mathrm{T}(n)+1 = 2\mathrm{T}(n-1)+2 = 2\left(\mathrm{T}(n-1)+1\right). \] Ainsi, \[ \mathrm{T}(n)+1 = 2\left(\mathrm{T}(n-1)+1\right) = 2\times 2\left(\mathrm{T}(n-2)+1\right) = \cdots = \underbrace{2\times\cdots\times 2}_{n\text{ fois}}\underbrace{\left(\mathrm{T}(0)+1\right)}_{=1}, \] ce qui implique que $\mathrm{T}(n)=2^n-1$.

Temps de résolution

Ainsi, si l’on suppose que le déplacement d’un disque est réalisé en une seconde, on peut résoudre le problème des tours de Hanoï à $n$ disques en $2^n-1$ secondes.

La tour de huit disques, représentée sur le croquis, peut être déplacée en $2^8-1=255$ secondes, soit $4$ minutes et $15$ secondes.

La tour de $64$ disques, dont il est question dans l’histoire « Les Brahmes tombent ! » de Lucas, nécessitent \[ 2^{64}-1 = 18\ 446\ 744\ 073\ 709\ 551\ 615 \] secondes soit plus de $584\ 554\ 531\ 243$ années.

Ce nombre gigantesque $2^{64}-1$ se retrouve également dans d’autres histoires. Par exemple, dans son texte, Lucas cite le jeu du baguenaudier ou encore la prétendue récompense faite à l’inventeur du jeu d’échecs.

Le nombre prodigieux que nous venons d’écrire se retrouve encore dans la théorie du baguenaudier de soixante-quatre anneaux. Ce nombre était connu des Indiens ; l’écrivain Asaphad rapporte, en effet, que Sessa, fils de Daher, imagina le jeu des échecs, où le roi, quoique la pièce la plus importante, ne peut faire un pas sans le secours de ses sujets, les pions, dans le but de rappeler au monarque indien Scheran les principes de justice et d’équité avec lesquels il devait gouverner. Scheran, enchanté d’une leçon donnée d’une manière si ingénieuse, promit à l’inventeur de lui donner tout ce qu’il voudrait pour sa récompense. Celui-ci répondit : « Que Votre Majesté daigne me donner un grain de blé pour la première case de l’échiquier, deux pour la seconde, quatre pour la troisième, et ainsi de suite en doublant jusqu’à la soixante-quatrième case. » Il aurait fallu huit fois la superficie de la Terre, supposée entièrement ensemencée, pour avoir en une année de quoi satisfaire au désir du modeste bramine. Le nombre de grains de blé est égal au nombre de déplacements de la tour d’Hanoï à soixante-quatre étages.

Une version simplifiée de la solution optimale.

La solution optimale présentée précédemment est définie de manière récursive. Nous allons ici simplifier sa définition.

Remarquons tout d’abord que dans la solution optimale, un mouvement sur deux concerne le plus petit disque. Ce résultat est facile à vérifier sur l’exemple précédent pour trois disques. Montrons-le de manière générale pour $n\geqslant 1$ disques :

• Si deux mouvements consécutifs concernent le plus petit disque, alors il est possible de remplacer ces deux mouvements par un seul. Si le plus petit disque est déplacé du piquet $X$ vers $Y$ et ensuite déplacé du piquet $Y$ vers $Z$, alors on considère directement le déplacement de ce disque du piquet $X$ vers le piquet $Z$. On réduit ainsi le nombre de mouvements total de un, ce qui contredit l’optimalité de la solution de départ.
• Il ne peut y avoir qu’un seul mouvement de disques entre deux déplacements du plus petit disque et ce mouvement est imposé par la position du plus petit disque. En effet, si le plus petit des $n$ disques est positionné sur le piquet $X$, alors on considère les disques $d_1$ et $d_2$ du dessus des deux autres piquets $Y$ et $Z$ (si l’un des piquets est vide, on considère le disque vide qui est de taille nulle). Le seul mouvement possible est donc de déplacer le plus petit des disques $d_1$ et $d_2$ au-dessus de l’autre. Pour le mouvement suivant, si l’on ne déplace pas le plus petit des $n$ disques, les disques $d_1$ et $d_2$ se retrouvent dans la position précédente, ce qui est impossible par optimalité de la solution. De plus, on remarque que ce déplacement du plus petit des disques $d_1$ et $d_2$ au-dessus de l’autre est imposé par la position du plus petit des $n$ disques sur le piquet $X$.

On considère maintenant les deux sens de déplacements $A\rightarrow B\rightarrow C\rightarrow A$ ou $A\rightarrow C\rightarrow B\rightarrow A$.

Pour déplacer les $n$ disques d’un piquet vers le piquet suivant dans le sens $S$ en utilisant $\mathrm{T}(n)$ mouvements, on procède de la manière suivante : si $n$ est impair, on déplace le plus petit disque une fois sur deux et toujours dans le sens $S$, si $n$ est pair, on déplace le plus petit disque une fois sur deux et toujours dans l’autre sens que $S$.

Ce résultat est évident pour $n=1$. Supposons qu’il soit vrai pour déplacer $\ n-1$ disques et montrons-le pour le déplacement de $\ n$ disques. Pour déplacer $\ n$ disques du piquet $X$ vers le piquet $Y$, en supposant que l’on considère le sens $\ S:X\rightarrow Y\rightarrow Z\rightarrow X$, et en utilisant $\ \mathrm{T}(n)$ mouvements, on procède ainsi :

Supposons que l’on déplace toujours le plus petit disque une fois sur deux et toujours dans le sens $\ S$. Puisque le résultat est supposé vrai pour $\ n-1$ disques et que $\ n-1$ est de parité inverse de $\ n$, les $n-1$ plus petits disques sont donc déplacés du piquet $X$ vers le piquet suivant dans l’autre sens que $S$, soit le piquet $Z$, par $\mathrm{T}(n-1)$ mouvements. Remarquons que $\mathrm{T}(n-1)$ est impair et que le mouvement suivant sera donc celui du plus grand disque qui sera déplacé du piquet $X$ vers le piquet $Y$. On continue les déplacements avec le plus petit disque et, toujours car l’on a supposé le résultat vrai pour $\ n-1$ disques et que $\ n-1$ est de parité inverse de celle de $\ n$, on déplace les $\ n-1$ plus petits disques du piquet $Z$ par le piquet suivant dans l’autre sens que $\ S$, soit le piquet $Y$, également par $\ \mathrm{T}(n-1)$ mouvements.

Au final, on a donc bien déplacé les $n$ disques du piquet $X$ vers le piquet $Y$ en $2\mathrm{T}(n-1)+1=\mathrm{T}(n)$ mouvements.

La solution optimale du problème des tours de Hanoï pour $n$ disques est ainsi obtenue par la méthode suivante : si $n$ est impair, on déplace le plus petit disque une fois sur deux toujours dans le sens $A\rightarrow C\rightarrow B\rightarrow A$, si $n$ est pair, on déplace le plus petit disque une fois sur deux toujours dans le sens $A\rightarrow B\rightarrow C\rightarrow A$.

Pour illustrer ceci, voici la solution optimale en $255$ mouvements du problème à $8$ disques où le plus petit disque, représenté en rouge, est toujours déplacé dans le sens $A\rightarrow B\rightarrow C\rightarrow A$.

La conjecture au prochain trimestre

Cela conclut cette présentation du problème classique des tours de Hanoï. Dans la seconde partie de cet article qui paraîtra le trimestre prochain, nous nous intéresserons à la généralisation de ce problème qui consiste à déplacer une tour de disques non plus à l’aide de trois piquets mais avec quatre piquets et plus. Nous énoncerons notamment la conjecture de Frame et Stewart qui porte sur le nombre optimal de mouvements de disque pour cette généralisation.

L’auteur tient à remercier les responsables de cette rubrique Shalom Eliahou et Bruno Martin, ainsi que les relecteurs Fabien Lange, Daniel Massart, QuentinB et ysf.zrir pour leur relecture attentive et leurs conseils avisés.

[ 1 ]  Henri de Parville, La Nature 566 (1884), p. 285.

[ 2 ]  E. Lucas, Récréations mathématiques, tome 3, p. 55-59, 1893.

Partager cet article

Pour citer cet article :.

Chappelon, Jonathan — «Les tours de Hanoï I : le problème classique» — Images des Mathématiques, CNRS, 2016

Commentaire sur l'article

Le 21 juin 2016 à 14:16, par projetmbc.

Merci pour cet article très bien rédigé.

Un souci par contre... Ne devrait-on pas associer une taille infinie à un piquet vide afin de pouvoir y déposer n’importe quel disque ? De plus d’un point de vus informatique, ceci permet de ne pas avoir à traiter différemment les piquets vides.

le 22 juin 2016 à 09:47, par Jonathan Chappelon

Merci pour votre message. Ici nous n’associons pas de taille aux piquets, uniquement les disques ont des tailles différentes. Je comprends toutefois en partie ce que vous voulez dire. On peut en effet supposer qu’à la base de chaque piquet il y ait un disque de taille infinie, ce qui permet de déposer n’importe quel autre disque de taille finie sur celui-ci. Personnellement je ne vois pas ce que cela peut apporter au problème et je ne pense pas que considérer des piquets vides en soit un non plus. Si je n’ai pas bien saisi ce dont vous vouliez parler, je vous remercie d’avance de préciser.

Dernière récurrence

Le 21 juin 2016 à 14:45, par projetmbc.

Il me semble que l’on doit commencer la récurrence à $n = 2$ car pour $n=1$ on a un seul mouvement et aucun des deux sens de parcours proposés ne permet d’aller directement de A à C. En espérant ne pas avoir dit de bêtises...

le 22 juin 2016 à 09:53, par Jonathan Chappelon

Merci pour votre commentaire. Nous parlons ici de la dernière preuve de l’article. Pour déplacer une tour de $n=1$ disque d’un piquet $X$ vers un piquet $Y$, il suffit de déplacer cet unique disque dans le même sens : du piquet $X$ au piquet $Y$. Pourriez vous expliquer plus en détails ce qui vous dérange avec ce cas ?

le 4 juillet 2016 à 20:25, par orion8

Résolution par un robot : https://www.youtube.com/watch?v=SEMfUE5K35I

le 3 décembre 2019 à 12:03, par hbx444

Pour 3 disques le déplacement de A->B->C ne marche pas puisque l’on obtient un nombre minimum de coup supérieur à 7. Alors comment on fait. Et si on doit faire un algo. récursif comment doit-on tenir compte de se problème.

Laisser un commentaire

Pour participer à ce forum, vous devez vous enregistrer au préalable. Merci d’indiquer ci-dessous l’identifiant personnel qui vous a été fourni. Si vous n’êtes pas enregistré, vous devez vous inscrire.

Connexion |  s’inscrire |  mot de passe oublié ?

Articles suggérés

Si vous avez aimé cet article, voici quelques suggestions automatiques qui pourraient vous intéresser :

Maître de Conférences, Institut de Mathématiques Alexander Grothendieck, Université de Montpellier.

Voir les commentaires (6)

L'image du jour.

Un article au hasard

Actualités des maths.

• 18 décembre 2023 Séminaire « Mathématiques et poésie, le fond et la forme » 7e séance le mercredi 20 décembre 2023
• 12 décembre 2023 Séminaire « Mathématiques et poésie, le fond et la forme » 6e séance le mercredi 13 décembre 2023
• 4 décembre 2023 Séminaire « Mathématiques et poésie, le fond et la forme » 5e séance le mercredi 6 décembre 2023
• 20 novembre 2023 Séminaire « Mathématiques et poésie, le fond et la forme » 4e séance le mercredi 22 novembre 2023
• 13 novembre 2023 Séminaire « Mathématiques et poésie, le fond et la forme » 3e séance le mercredi 15 novembre 2023
• 6 novembre 2023 Journée Tangente 2023 le 3 décembre 2023

• Jeux & Activités
• Cadeaux Femme
• Cadeaux Homme

Pour ajouter ce produit à vos listes, connectez-vous à votre compte.

• Jeux, jouets
• Jeux de société
• Casse-têtes

Top Vendeur

• - Engagement et valeurs communes à Nature & Découvertes
• - Délai d'acceptation des commandes inférieur à 24h
• - Taux d'incident inférieur à 3%
• - Taux d'acceptation des commandes supérieur à 98%
• - Délai moyen de réponse aux clients inférieur à 48h
• - Note moyenne supérieure à 4,3/5
• - Délai d'expédition inférieur à 48h
• - Vendeur actif depuis plus de 6 mois sur la Marketplace

Casse-tête tour de Hanoï

Ref. 30163620

La livraison s'effectue devant votre domicile (à l'entrée de votre immeuble, devant le portail de votre maison). Découvrez toutes les conditions d'expéditions et modes de livraison

1 - Je choisis mes articles et le magasin de retrait sur natureetdecouvertes.com en cliquant sur RETIRER EN MAGASIN dans la fiche article. 2 - Je valide ma commande et je paye en ligne. 3 - Je reçois un sms et un e-mail de confirmation dès que ma commande est prête en magasin (disponible sous 1H, dans la limite des horaires d'ouverture du magasin). 4 - Je récupère ma commande en magasin sous 4 jours ouvrés, sans faire la queue en caisse ! En savoir plus

En commandant avant 16h du lundi au vendredi, votre commande sera expédiée le jour même. Découvrez toutes les conditions d'expédition et modes de livraison

Vous avez 30 jours pour changer d'avis tout simplement ! Effectuez votre retour gratuit en déposant votre colis dans un bureau de poste ou dans l’un des 7 500 points de dépôt Colissimo mis à votre disposition. Votre retour sera traité sous 15 jours ouvrés environ à compter de la date de réception de votre colis. En savoir plus

• Vendu et expédié par Nature & Découvertes

Sous 30 jours

La tour de Hanoï est un célèbre casse-tête inventé par un mathématicien français, Édouard Lucas.

• Le but ? Déplacer tous les disques de la tour de départ vers la tour d'arrivée, en utilisant la tour intermédiaire pour s'aider.
• Attention : on ne peut déplacer qu'un seul disque à chaque coup ; et il faut toujours poser un disque sur un disque plus grand que lui. Alors, place au défi !

Caractéristiques : Fabriqué en bois de bouleau. H. 6,8 cm - l. 5 cm - L. 14 cm.

• ATTENTION ! Ne convient pas aux enfants de moins de 3 ans.
• Référence 30163620

Casse-tête

De 15 à 30 minutes

Casse-tête STEM

Top 10 du rayon Jeux de société

• Bascule d'Archimède
• Gagne ton papa !
• Kapla défi
• Jeu d'échecs pliable (41 x 41 cm)
• Premier verger
• Bingo de luxe
• Jeu de palets - plateau réversible
• Le double tangram cœur

Click & collect

Gratuit sous 1h

Livraison offerte

Dès 49 € d’achat*

Retours gratuits

sous 30 jours*

Paiement sécurisé

CB, Paypal, Paiement en 3x

Les tours de hanoï sont un casse-tête très ancien. Trois piquets sont plantés côte à côte sur le sol. Sur le premier piquet sont enfilés des disques de bois de différentes tailles, du plus grand au plus petit.

Voici une illustration d'un jeu de tours de Hanoï composé de 9 disques :

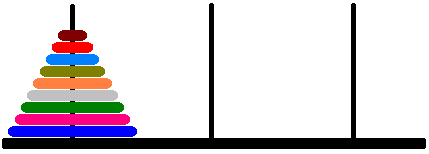
Le but du casse-tête est de déplacer l'ensemble de la pile de disques vers le troisième piquet. Un coup consiste à déplacer un disque du sommet d'un piquet vers le sommet d'un autre piquet, en respectant la règle suivante :

Un disque ne peut jamais être placé sur un disque plus petit que lui.

Illustration de l'état du jeu après quelques coups :

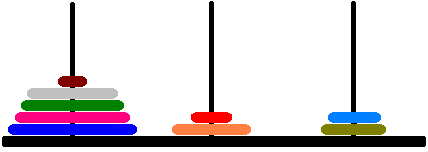
Limites de temps et de mémoire (Python)

• Temps : 1 s sur une machine à 1 GHz.
• Mémoire : 1 000 ko.

Contraintes

• 1 N N est le nombre de disques.

Vous devez lire un entier sur l'entrée standard : le nombre de disques se trouvant sur le piquet 1 au départ.

Vous devez écrire une ligne sur la sortie par déplacement permettant d'arriver à la solution finale (dans l'ordre où ils doivent être effectués).

Chaque déplacement est décrit par le numéro du piquet duquel un disque est retiré, le texte " -> ", puis le numéro du piquet sur lequel le disque est placé. Les piquets sont numérotés de 1 à 3.

Commentaires

Une fois que l'on a trouvé le principe, le casse-tête se résout toujours de la même manière, assez simplement. Si vous ne trouvez pas, demandez les conseils automatiques avant d'essayer de programmer une solution compliquée.

Vous devez être connecté(e) pour résoudre ce problème.

L'inscription ne prendra qu'une minute et vous pourrez alors résoudre les exercices puis faire valider automatiquement vos solutions.

Une fois identifié(e), vous pourrez demander sur cette page des conseils pour résoudre le sujet ou demander de l'aide sur le forum d'entraide.

Lorsque vous serez connecté(e), vous pourrez voir vos actions ici.

Une correction détaillée sera disponible lorsque vous aurez résolu le sujet.

Correction en cours de chargement…

SOYEZ LE PREMIER À SAVOIR

Bénéficiez immédiatement d'une réduction de 10 % et inscrivez-vous à la newsletter Logica Giochi pour recevoir des mises à jour en temps opportun sur vos produits préférés!

Javascript est désactivé dans votre navigateur. Pour une meilleure expérience sur notre site, assurez-vous d’activer JavaScript dans votre navigateur.

• LOGICA GIOCHI B2B

• Créer un compte
• Suivre vos commandes
• Conditions Générales de Vente
• Retours et remplacements
• Contactez-nous
• Programme d'affiliation
• Distribution
• Logica Jeux sur les réseaux sociaux
• Mentions légales
• Nous contacter
• Afficher les prix
• Incl. VAT Excl. VAT
• Comparer ( )

FUITE DE LA PRISON - Khun Phaen - L'Âne rouge

TOUR DE HANOÏ

• Un des casse-têtes les plus anciens dans le monde: la légende millénaire indienne rend ce jeu très intrigant
• Jeu séquentiel de différentes difficultés. 9 DISQUES
• Differentes difficultées en fonction du numéro des disques utilisés. RÈGLES INCLUSES en FR, DE, ES, ENG, IT
• Bois Teak/Samena. Bois naturel. Fabriqué en Thaïlande avec du bois provenant de bois régénérés (un arbre coupé = un arbre planté)
• Dimensions ouvert: 21x13x9 cm. Dimensions du jeu fermé dans la boîte: 21x3,5x9 cm

Un des casse-têtes les plus anciens dans le monde: la légende millénaire indienne rend ce jeu très intrigant

Disponibilité : En stock

Disponible 1.838 pieces

FRAIS DE LIVRAISON

PRÉPARATION RAPIDE: 24 H

Livraison dans ue gratuite >69€ *, prix sans tva hors ue voir les prix réduits sans tva, en sélectionnant l'option excl.vat dans le menu du compte *ou connectez-vous et définissez votre adresse de livraison pour voir les prix réduits, paiement sécurisé.

• Retour sur Futura

• Futura-Sciences : les forums de la science
• MATHEMATIQUES
• Mathématiques du supérieur

Dénombrement et combinaisons ( tour de hanoï)

Bonjour, J’ai de mal à répondre aux questions suivantes Sachant qu'on part d'une tour de Hanoï. 3 tours et n disques Soit Sn la suite de coups permettant de déplacer les n disques d'une tour vers une autre. On note cn le nombre de coups de Sn Question 1 Combien existe-t-il de façons de placer les 9 disques de sorte à ce qu'il y ait 3 disques sur chaque tour. On ne considérera que les placements corrects. Question 2 Combien existe-t-il de façons de placer sur les trois tours : — n disques de manière correcte ? — n disques, éventuellement de manière incorrecte ? Question 3 On souhaite maintenant coder un placement correct de n disques sur les trois tours. Peut-on coder ce placement avec 2n bits ? Justifiez votre réponse. Question 4 Combien existe-t-il de façons de placer les 6 disques de sorte à ce qu'il y ait 2 disques sur chaque tour. On considérera cette fois-ci tous les placements possibles même ceux qui ne sont pas corrects. Cela signifie que les disques ne sont pas forcément empilés par taille décroissante de bas en haut. Deux placements sont différents si on peut trouver un disque qui n'est pas à la même position (en partant du haut) dans une tour dans les deux placements ou si on peut trouver un disque qui n'est pas sur la même tour dans les deux placements. Question 5 On souhaite maintenant coder un placement (pas nécessairement correct) de n disques sur les trois tours. Peut-on coder ce placement avec 2n[log(n)] bits ? En cas de réponse positive donner le codage et en cas de réponse négative donner un argument prouvant l'impossibilité d'un tel codage.

Re : Dénombrement et combinaisons ( tour de hanoï)

bonsoir, tu pourrais commencer par nous dire ce que tu as essayé de faire. déjà pour la première question.! cordialement.

y'a quelque chose qui cloche là dedans, j'y retourne immédiatement !

pour la première

Pour la question 2)a), on peut s’intéresser, pour chaque disque, au numéro de la tour sur laquelle il se trouve. Pour la question b), c'est un peu plus sournois. une façon de faire, c'est de représenter la situation par une liste des numéro des disques avec deux séparateurs à placer. Par exemple, on pourra représenter la situation Code: 5 1 2 3 4 Par 2 1 5 | 3 | 4 A partir de là, il n'est pas trop difficile de calculer le nombre de telles listes (combien de listes de n nombres? Combien de façon de placer deux séparateurs (pouvant être collés !) dans une liste?)

edit : à mieux re exprimer

Dernière modification par ansset ; 17/03/2017 à 00h03 .

pour le 2)a) ce n'est pas : ? pour b) c'est un exemple de 5 disques ?

un doute pour la première : ne manque t il pas un facteur 3! qui correspond aux combinaisons des tours ?

par exemple pour 5 disque on a 3^ 5 non

pour les deux réparateurs j'ai trouvé une combinaison de 2 paris 7

Envoyé par miido pour le 2)a) ce n'est pas : ? pour b) c'est un exemple de 5 disques ? Oui et oui Envoyé par ansset un doute pour la première : ne manque t il pas un facteur 3! qui correspond aux combinaisons des tours ? Non : dès que tu fixes les disques par tour, il n'existe qu'un seul placement correct (les disques doivent nécessairement être rangés dans l'ordre sur chaque tour pour que le placement soit valide) Envoyé par miido pour les deux réparateurs j'ai trouvé une combinaison de 2 paris 7 Non, car les deux séparateurs peuvent être à la même position (ça correspond à une tour vide) : Code: 5 1 3 2 . 4 Correspond à : 2 1 5 | | 4 3

Envoyé par Tryss2 Non : dès que tu fixes les disques par tour, il n'existe qu'un seul placement correct (les disques doivent nécessairement être rangés dans l'ordre sur chaque tour pour que le placement soit valide) OK, faut que je revois précisément les règles.

Bonjour pour la question 4 j'ai trouvé : c'est juste ?

Envoyé par miido pour le 2)a) ce n'est pas : ? pour b) c'est un exemple de 5 disques ? Pour la première question je trouve 1680 aussi. Pour le 2 a) je prends un n multiple de 3 sinon il y a un reste c'est plus compliqué, je trouve plutôt

Et pour le 2 b) juste n!

Pour le 2a je confirme "> Pour le 2b je trouve

Dernière modification par Médiat ; 17/03/2017 à 17h15 .

Je suis Charlie. J'affirme péremptoirement que toute affirmation péremptoire est fausse

Envoyé par redrum13 Pour la première question je trouve 1680 aussi. Pour le 2 a) je prends un n multiple de 3 sinon il y a un reste c'est plus compliqué, je trouve plutôt Mauvaise compréhension de la question ne pas tenir compte de ma réponse du 2 a)

Pour la 3) par contre je dirais (avec prudence) que le nombre de codages est supérieur au nombre de bons placements des n disques: donc oui.

Pour la 4) 6! (produit des arrangements de 2 parmi 6 en décrémentant de 2)

Envoyé par redrum13 Pour la 4) 6! (produit des arrangements de 2 parmi 6 en décrémentant de 2) Ou directement 6! (on prend une permutation quelconque, on met les 2 premiers éléments sur la première pique , les 2 suivants sur la deuxième et les 2 derniers sur le 3ième)

Pour la 2 b) je tombe sur al même chose: 3 placements au premier disque, 4 placements possibles pour un deuxième disque, 5 pour un troisième etc qque soit la configuration par piquet, soit 3*4*5*...*(n+2)= C'est comme rajouter un piquet de plus à chaque fois non?

Dernière question comparer 2n(log(n)) avec 0.5(n+2)! factorielle croit plus vite que n.log(n) d'après mes souvenirs de complexité

Dernière modification par redrum13 ; 17/03/2017 à 20h27 .

A priori 0.5(n+2)! > 2n(log(n)) pour tout entier n,donc le codage ne suffit pas.

Discussions similaires

Analyse combinatoire: dénombrement-permutations-arrangements-combinaisons, tour d'hanoi, problème : la tour de hanoï, combinaisons/denombrement, help.

À propos des cookies sur ce site

Ce site utilise des cookies pour améliorer votre expérience en ligne. Si vous continuez à utiliser ce site sans modifier vos préférences de cookies, nous en conclurons que vous marquez votre accord quant à notre utilisation de cookies. Pour en savoir plus ou pour modifier vos préférences de cookies, consultez notre politique relative aux cookies

CogniFit - Test de la tour de Hanoï

Pour mon propre entraînement

Pour suivre des patients

Pour un membre de ma famille

Pour suivre des élèves

Pour des recherches

Bien-être des employés

Développeurs

Vous allez créer un compte personnel. Ce type de compte est conçu pour vous aider à évaluer et à entraîner vos capacités cognitives.

Vous allez créer un compte de gestion des patients. Ce compte a pour vocation d'aider les professionnels de santé (médecins, psychologues...) dans le diagnostic et la stimulation cognitive.

Vous allez créer un compte familial. Ce compte est conçu pour permettre aux membres de votre famille d'accéder aux évaluations et aux entraînements de CogniFit.

Vous allez créer un compte de recherche. Ce compte est spécialement conçu pour aider les chercheurs dans leurs études dans les domaines cognitifs.

Vous allez créer un compte de gestion des étudiants. Ce compte est conçu pour aider au diagnostic et à l'intervention des troubles cognitifs chez les enfants et les jeunes étudiants.

Vous allez créer un compte de gestion d'entreprise. Ce compte est conçu pour permettre à vos employés d'accéder aux évaluations et à la formation CogniFit.

Vous allez créer un compte développeur. Ce compte est conçu pour intégrer les produits CogniFit au sein de votre entreprise.

Pour votre propre usage (à partir de 16 ans)

Envoyez des évaluations et des entraînements à vos patients

Envoyez des évaluations et des entraîenements à vos étudiants

Envoyez des évaluations et des entraînements à vos enfants ou vos proches

Envoyez des évaluations et des entraînements aux personnes participant à vos recherches

En cliquant sur "Inscrivez-vous", vous acceptez nos Conditions d’utilisation et vous reconnaissez avoir lu et accepter notre Politique de Confidentialité des données.

Les références

Hinz, A. (1989). "The Tower of Hanoi". L'Enseignement Mathématique. 35: 289–321. doi:10.5169/seals-57378.

App CogniFit

• Nous suivre

Votre cerveau

• Cerveau et esprit
• A propos du cerveau
• Les parties du cerveau
• Plasticité neuronale
• Perte de Mémoire
• Déficience intellectuelle
• Functions cérébrales
• Validation thérapeutique numérique
• Jeux d'ordinateur
• Adultes en bonne santé
• Évaluation holistique
• Personnes âgées en bonne santé (iTV)
• Entraînement adultes âgés
• État cognitif chez les personnes âgées
• Révision systémique
• Taxonomie SG4D
• Jeux pour le cerveau
• Échecs en ligne
• Mini-mots croisés
• Fruit Frenzy
• Crystal Miner
• Robo Factory
• Neon Lights
• Rends moi fou
• mots croisés visuels
• Faîtes la paire
• Space Rescue
• Chaos mathématique
• Course de billes
• Tennis mélodique
• Trouvez votre animal de compagnie
• Paires musicales
• Chronocolor
• Aventures de grenouille
• Pingouin Explorateur
• Abeille de Couleur
• Jeux d'agilité mentale
• Jeux en ligne pour la mémoire
• Développement cognitif
• Exercice cérébral
• Quizz pour la tête
• Exercices pour l'esprit
• Entraînement cérébral personnalisé
• Exercice mental
• Jeux mathématiques amusants
• Batailles cérébrales
• Conditions d'utilisation
• Confidentialité
• La Direction de CogniFit
• Salle de presse
• Devenir un affilié
• Nous contacter

Veuillez entrer votre adresse email

Recueil d'exercices pour apprendre Python au lycée

Tours de Hanoï

Difficulté : moyenne

Les tours de Hanoï est un casse-tête composé de trois tours et une pile de disques rangés du plus grand au plus petit comme sur la photo ci-dessous .

Le but est de déplacer la pile de disques sur la tour de droite en ne déplaçant à chaque fois qu'un seul disque et un disque ne peut pas être posé sur un disque plus petit. Voici une animation de ce qu'il faut faire dans le cas où il y a 4 disques.

On peut aller voir Wikipédia par exemple pour plus d'informations.

Nous allons voir qu'il est très simple de créer un programme récursif qui nous dit quoi faire pour résoudre le problème. Tout d'abord on appelle les tours A, B et C. On appelle n le nombre de disque présents au départ dans la tour A. Pour déplacer tous les disques de la tour A vers la tour C, on peut raisonner comme suit :

• On déplace n-1 disques de A vers la tour B
• On déplace le dernier disque de A vers C
• On déplace les n-1 disques de B vers C

L'astuce ici est de créer une fonction hanoi qui prend 4 paramètres : hanoi(n,debut,inter,fin) où n est le nombre de disques à déplacer, debut est la tour de départ de nos n disques, inter est la tour intermédiaire que l'on peut utiliser pour déplacer et fin est la tour ou doivent se trouver les n disques au final.

Ainsi, au début on va lancer hanoi(n,"A","B","C") mais quand on va vouloir déplacer les n-1 disques de A vers B, on écrira hanoi(n-1,"A","C","B") .

Ecrire cette fonction recursive hanoi(n,debut,inter,fin) de manière à afficher (avec print ) à chaque étape le déplacement à effectuer sous la forme "A B" pour un déplacement de la tour "A" vers la tour "B" par exemple.

Entrée : (n,"A","B","C") où n est un entier.

Sortie : Les instructions à suivre pour déplacer les n disques de la tour "A" à la tour "C" donnée sous la forme "A B" pour signifier un déplacement de A vers B et affiché avec print .

Les bases de Python pour le lycée

Apprendre les bases de python pour réussir en n.s.i., python pour le collège et le lycée. exercices, cours, tp, projets., apprendre python dans le secondaire.

The #1 tech hiring platform